He estado trabajando gradualmente en el desarrollo desde cero de herramientas para probar el rendimiento de los sistemas de bases de datos de código abierto. Uno de los componentes de este kit de herramientas es un generador de datos capaz de crear conjuntos que serán cargados en una base de datos. Necesitaré un generador de números aleatorios que cuente con las siguientes características importantes:
- replicabilidad de los datos
- velocidad de ejecución
La capacidad de reproducir los mismos datos puede ser importante cuando un determinado conjunto de datos provoca algún evento interesante. En el transcurso de una prueba, los datos pueden cambiar, así que necesitaba poder volver a empezar con un conjunto idéntico. Otra situación para la cual hay que estar preparado es cuando el tamaño del conjunto de datos es tan grande que resulta imposible guardar una copia de los datos sin formato, y mucho menos un respaldo de la base de datos.
El rendimiento puede resultar en un importante ahorro de tiempo al manejar grandes cantidades de datos. Si hacen falta 24 horas para generar 10.000 millones de filas de datos, una mejora del 20% en la velocidad de ejecución se traduce en casi 5 horas de ahorro de tiempo. Ya sea en forma de algoritmos utilizados o de lenguaje de programación, la suma de muchas pequeñas mejoras puede convertirse en un ahorro de tiempo considerable cuando se requieren días o incluso más tiempo. La cifra del 20% es solamente un ejemplo, así que es necesario evaluar lo que podemos esperar.
El siguiente paso es escoger el generador de números aleatorios que emplearemos. En este caso usaremos un generador de números pseudoaleatorios, por dos razones específicas: es más rápido que un simple generador de números aleatorios y se supone que sus resultados sean reproducibles.
Empecé con unas clases sobre los generadores de números pseudoaleatorios ya disponibles en C (y Rust, aunque me gustaría hablar más de este último en otra ocasión) con una licencia compatible con la de PostgreSQL:
Quiero evaluar estos generadores en función de tres propiedades específicas, para ver cómo pueden afectar a mis necesidades:
- ¿Cuánto tiempo tardan en generar los números?
- ¿Cuánto tiempo tardan en inicializar el generador?
- ¿Es posible avanzar el generador sin la necesidad de generar números?
Equinix Metal proporcionó al Grupo Global de Desarrollo de PostgreSQL el equipo que me permitió realizar algunas de estas pruebas. El sistema proporcionado cuenta con una CPU Intel(R) Xeon(R) de 48 núcleos E5-2650 con 250GB de RAM. Los generadores de números pseudoaleatorios en sí mismos no sobrecargan el sistema. De todas formas, esperamos poder comprobar cómo se desempeñará más adelante un generador de datos aleatorios.
La primera prueba realizada mide la rapidez con la cual pueden generarse 10.000 millones de números aleatorios:
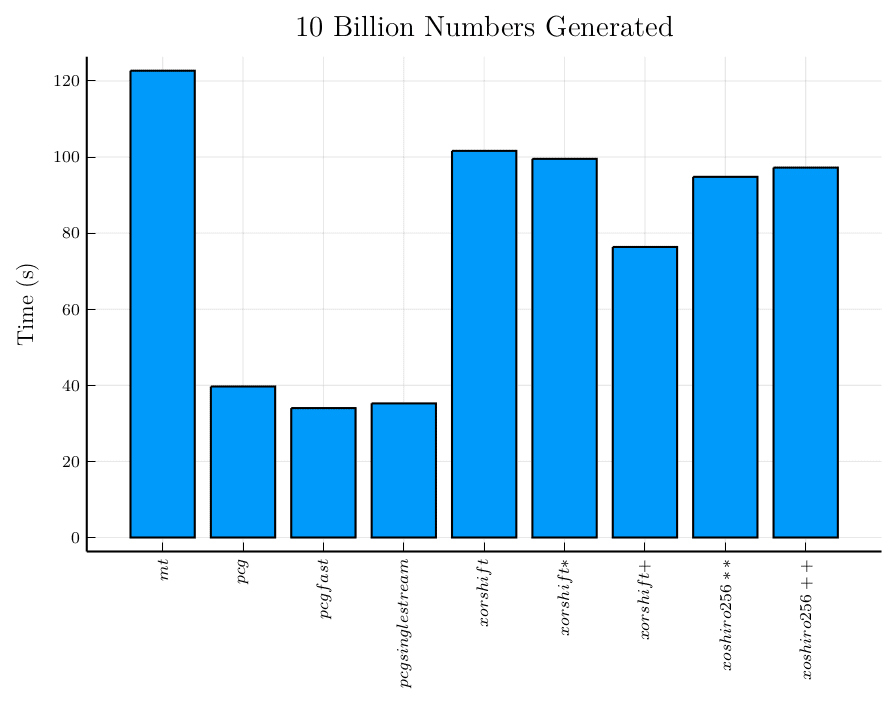
Los generadores congruentes permutables pueden generar números a una velocidad más del doble que cualquiera de los generadores de registro de desplazamiento, y tres veces más rápida que la del generador Mersenne Twister. Esta parece ser una buena razón para seguir experimentando con estos generadores y averiguar su impacto en el rendimiento general de un generador de datos aleatorios.
Ahora, analicemos lo que conlleva inicializar un generador. La razón es determinar cómo crear un generador de datos aleatorios que genere datos consistentes.
Un método a considerar consiste en introducir los datos en el generador por filas en una tabla. Así que, al paralelizar el generador de datos, sabremos exactamente dónde iniciarlo.
Una razón adicional es que nos permite usar un nuevo generador para una columna de datos específica, como por ejemplo, cualquier columna que necesite una cantidad variable de números generados. Para producir un resultado, la distribución Gaussiana emplea una cantidad no determinante de números aleatorios. Una cadena aleatoria utiliza un número aleatorio para la longitud de la cadena y otro por cada carácter de la cadena.
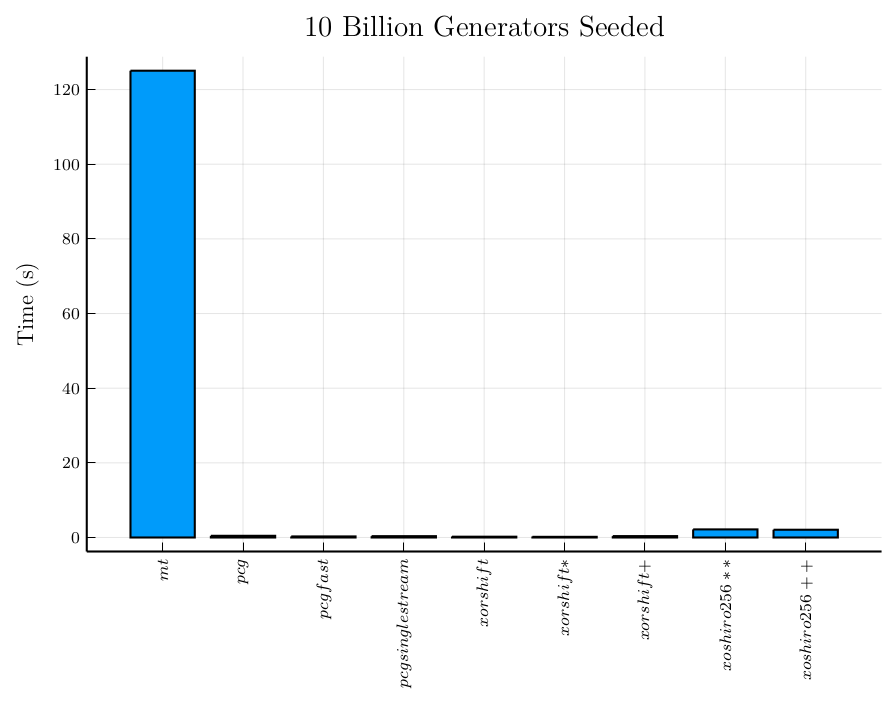
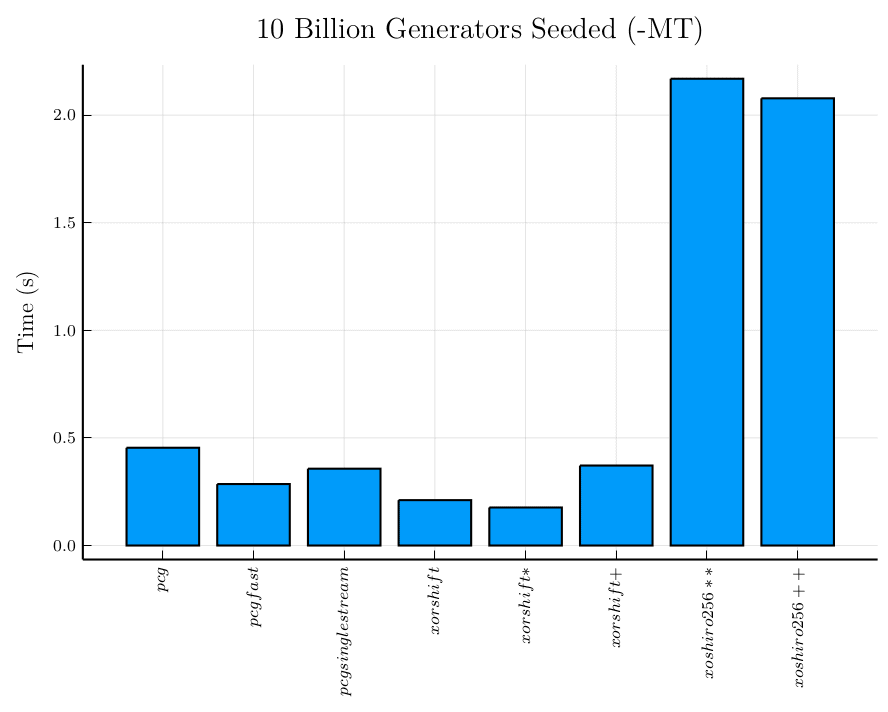
Aquí les presento dos gráficos: con y sin el generador Mersenne Twister. Inicializar el generador Mersenne Twister resulta dos órdenes de magnitud más lento que iniciar cualquiera de los otros generadores. Por eso quise analizar mejor los demás generadores sin el Mersenne Twister. Los generadores de registro de desplazamiento varían un poco entre ellos, mientras que los generadores congruentes permutables parecen ser más consistentes y están en el mismo orden de magnitud que los generadores de registro de desplazamiento más rápidos.
Por otra parte, la inicialización de los generadores de registro de desplazamiento y de los generadores congruentes permutables resulta un orden de magnitud más rápida que su respectivo tiempo de generación de números.
Los generadores congruentes permutables cuentan con una funcionalidad añadida que permite avanzar el generador hasta un punto específico, facilitando así la paralelización del mismo generador de datos.
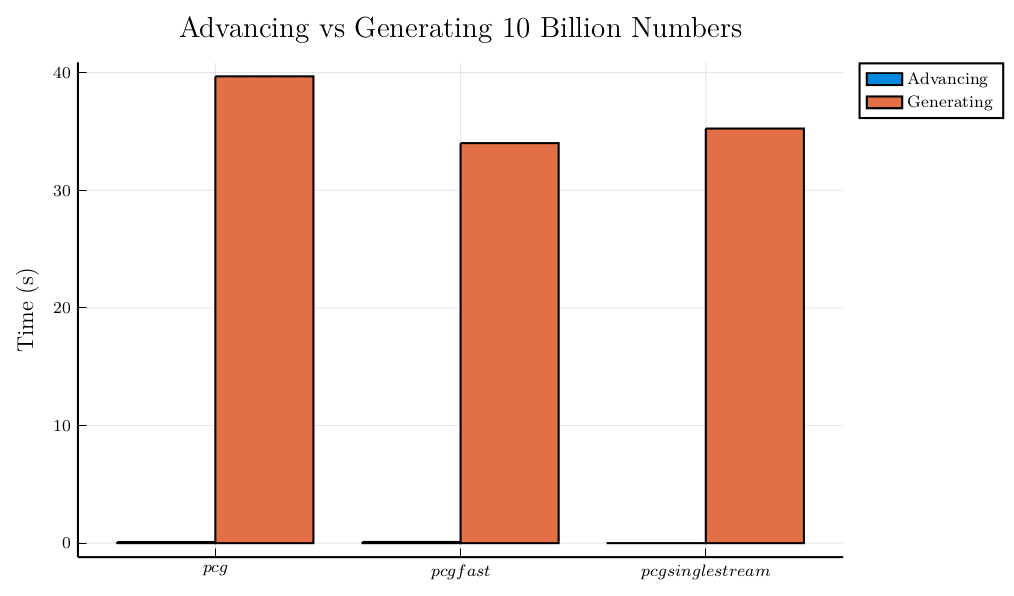
La llamada de función que permite avanzar el generador de 10 mil millones de números, en lugar de generar la misma cantidad, supone una diferencia de un par de órdenes o magnitud en cada caso.
Los resultados de estas pruebas me sugieren que los generadores congruentes permutables presentan un mejor equilibrio general de rendimiento entre la inicialización, la generación y el paralelismo en un generador de datos. Sin embargo, la verdadera prueba versará sobre el real impacto que estas diferencias tendrán en el mismo generado.
